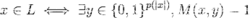NP-hard

编辑

其中，NP 是指非确定性多项式（non-deterministic polynomial，缩写 NP）。所谓的非确定性是指，可用一定数量的运算去解决多项式时间内可解决的问题。

例如，著名的推销员旅行问题（Travel Saleman Problem or TSP）：假设一个推销员需要从香港出发，经过广州，北京，上海，…，等 n 个城市， 最后返回香港。 任意两个城市之间都有飞机直达，但票价不等。假设公司只给报销 C 元钱，问是否存在一个行程安排，使得他能遍历所有城市，而且总的路费小于 C？

推销员旅行问题显然是 NP 的。因为如果你任意给出一个行程安排，可以很容易算出旅行总开销。但是，要想知道一条总路费小于 C 的行程是否存在，在最坏情况下，必须检查所有可能的旅行安排！ 这将是个天文数字。

旅行推销员问题是数图论中最著名的问题之一，即“已给一个 n 个点的完全图，每条边都有一个长度，求总长度最短的经过每个顶点正好一次的封闭回路”。Edmonds，Cook 和 Karp 等人发现，这批难题有一个值得注意的性质，对其中一个问题存在有效算法时，每个问题都会有有效算法。

迄今为止，这类问题中没有一个找到有效算法。倾向于接受NP 完全问题（NP-Complete 或 NPC）和 NP 难题（NP-Hard 或 NPH）不存在有效算法这一猜想，认为这类问题的大型实例不能用精确算法求解，必须寻求这类问题的有效的近似算法。

此类问题中，经典的还有 子集和问题； Hamilton 回路问题；最大团问题

形式化定义

编辑

常用的定义是所谓的“关系定义式”。即对于一个语言 L，L 在 NP 中，那么存在多项式时间图灵机 M，和多项式 p 使得

词条标签：

科学 ， 学科