作为量子力学的基础方程之一，薛定谔方程一直广受关注。去年，DeepMind 科学家开发一种新的神经网络来近似计算薛定谔方程，为深度学习在量子化学领域的发展奠定了基础。今年九月份，柏林自由大学的几位科学家提出了一种新的深度学习波函数拟设方法，它可以获得电子薛定谔方程的近乎精确解。相关研究发表在 Nature Chemistry 上。

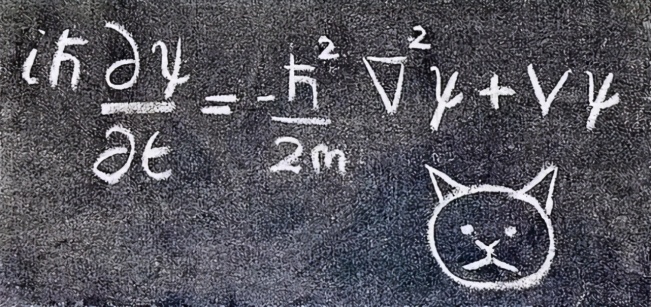
即使并非物理学界人士，我们也对薛定谔这个名字并不陌生，比如「薛定谔的猫」。著名物理学家埃尔温 · 薛定谔是量子力学奠基人之一，他在 1926 年提出的薛定谔方程（Schrödinger equation）为量子力学奠定了坚实的基础。薛定谔方程是描述物理系统的量子态怎样随时间演化的偏微分方程，是量子力学的基础方程之一。

在经典力学里，人们使用牛顿第二定律描述物体运动。而在量子力学里，类似的运动方程为薛定谔方程。薛定谔方程的解完备地描述物理系统里微观尺寸粒子的量子行为，包括分子系统、原子系统、亚原子系统。微观系统的状态由波函数来描写，薛定谔方程即是波函数的微分方程。若给定了初始条件和边界的条件，就可由此方程解出波函数。另外，薛定谔方程的解还可完备地描述宏观系统，可能乃至整个宇宙。

求解薛定谔方程可以为化学反应提供线索。化学反应的结果基本上与电子以及它们环绕原子和分子的方式有关。而控制事物反应的能量以及电子在分子中的轨道的差异决定了化学物质的形状，也由此决定了其性质。计算这一能量的方式就是求解薛定谔方程。换句话说，求解出薛定谔方程，就可以知道化学反应的结果。

然而，这并非易事。此前，我们可以精确求解的原子只有氢原子——仅具备一个质子和一个电子。

最近，来自柏林自由大学的科学家提出利用人工智能计算薛定谔方程的基态解，相关研究发表在 Nature Chemistry 上。

用 AI 求解薛定谔方程

量子化学旨在预测分子的化学和物理性质，它仅利用分子在三维空间中的原子排列来完成。这可以减少对资源的需求，并加快实验速度。理论上，这可以通过求解薛定谔方程来完成，但在实践中这往往非常困难。目前，人们仍无法高效求得任意分子的精确解。

最近，来自柏林自由大学的科学家提出一种深度学习方法，达到了前所未有的计算效率和准确度权衡。

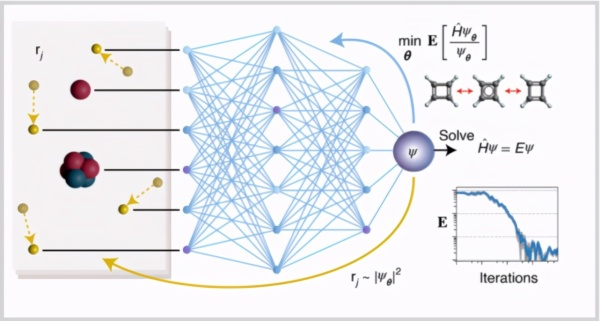
该研究作者之一 Frank Noé 教授表示：「我们认为这一方法或将极大地影响量子化学的未来。」

无需在准确度和计算成本之间做出取舍

波函数是量子化学和薛定谔方程的关键所在，是一种描述分子内电子行为的函数。它是一种高维实体，这使得捕获编码特定电子之间相互影响方式的频谱变得极度困难。

量子化学领域中的许多方法不再只是尝试以数学方式获得特定分子的能量，但这需要近似值，限制了预测的质量。还有一些利用大量简单数学构造块表示波函数的方法，但这些方法过于复杂，难以针对较多原子计算波函数。

该研究一作 Jan Hermann 设计了新方法的关键特征，他表示：「避免在准确度和计算成本之间进行权衡是量子化学的最高成就。」

将物理属性引入 AI 神经网络

Hermann 表示：「到目前为止，最流行的方法是极具成本效益的密度泛函理论。我们认为我们提出的深度『Quantum Monte Carlo』方法至少可以达到同样好的效果。该方法以可接受的计算成本提供了前所未有的准确度。」

该研究设计了一个深度神经网络来表示电子的波函数，这是一种全新的方法。Noé 解释说：「我们没有使用用相对简单的数学成分组成波函数的标准方法，而是设计了一种人工神经网络，它能够学习电子围绕原子核运动的复杂模式。」

Hermann 表示：「电子波函数的独特性在于反对称性。在交换两个电子时，波函数需要改变符号，我们必须将这种特性引入到神经网络架构中才能使之奏效。」

受泡利不相容原理启发，PauliNet 方法诞生

受到「泡利不相容原理」（Pauli exclusion principle）的启发，研究者将他们的方法命名为「PauliNet」。它是一种深度学习波函数拟设，可以获得电子薛定谔方程的近乎精确解。PauliNet 具有一个作为基线的内置多参考哈特里－福克（Hartree–Fock）解，集成有效波函数的物理特性，并使用变分量子蒙特卡罗方法（variational quantum Monte Carlo, VMC）进行训练。

PauliNet 拟设架构的信息流如下图所示：

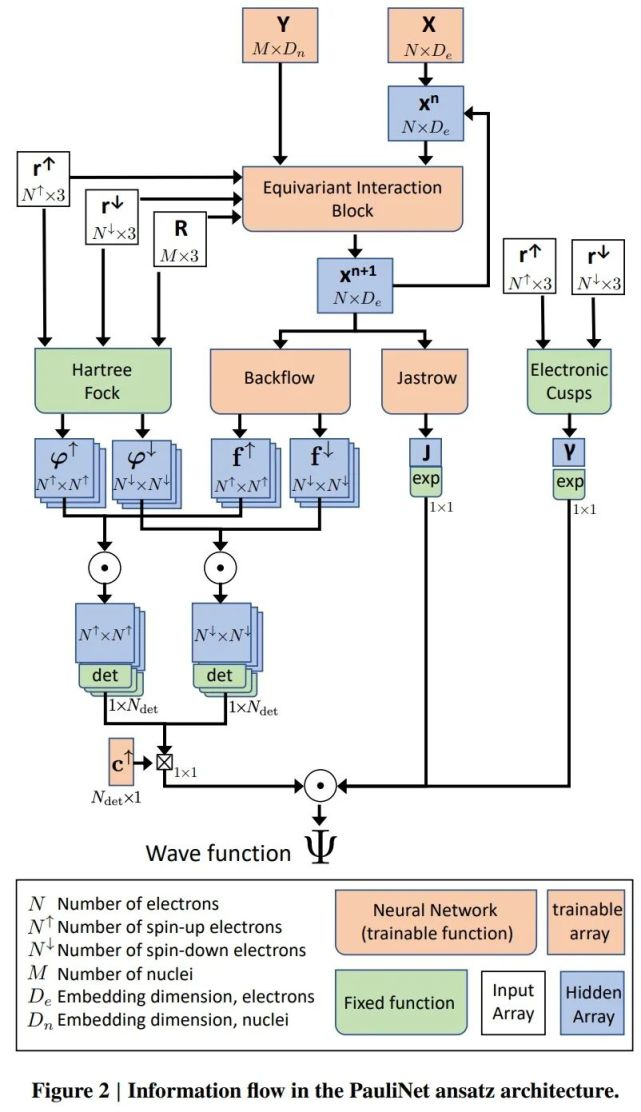
在实验部分，研究者采用了用于 DeepWF（Han et al., 2019）的相同系统，具体为氢分子（H_2）、氢化锂（LiH）、铍（Be）以及硼（B）和线性氢链 H_10。研究者将 PauliNet 与 SD-VMC（singledeterminant variational, 标准单行列式变分蒙特卡罗）、SD-DMC（singledeterminant diffusion, 标准单行列式扩散蒙特卡罗）和 DeepWF 进行了比较。

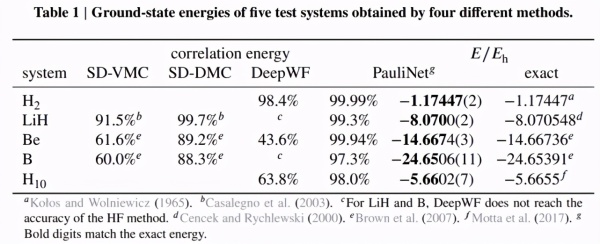
结果表明，PauliNet 的性能优于这三种用于原子、双原子分子和强相关氢链的 SOTA VMC 拟设方法，并且具有较高的计算效率。下表 1 为使用这四种不同方法时，H_2、LiH、Be、B 和 H_10 五种系统的基态能量对比：

求解薛定谔方程的潜在应用

研究者预计，由于系统大小对实验效果具有正面影响，该方法可能成为中型分子系统上高准确度电子结构计算的新主导方法。

当然，在本研究提出的新方法能够处理工业应用之前，研究者还有很多需要克服的难题。研究者表示：「这是一项基础性研究，但对于分子和材料科学中的古老问题而言却是一种最新方法。我们很高兴该方法创造了无限的可能性。」

求解薛定谔方程在量子化学领域具有广泛的应用。从计算机视觉到材料科学，求解薛定谔方程将会促成人类想象不到的商品发展。虽然这一革命性创新离落地应用还有很长的一段路要走，但这一研究活跃在科学世界依然令人兴奋。